Influencing factors and measurement methods of lithium battery self-discharge

The self-discharge reaction of lithium-ion batteries is inevitable, and its existence not only leads to the reduction of the battery's own capacity, but also seriously affects the sorting and matching of the battery cell and the cycle life of the battery pack.

The self-discharge rate of lithium-ion batteries is generally 2% to 5% per month, which can fully meet the requirements of the single battery cell.

However, once the single lithium battery cell is assembled into a module, because the characteristics of each single lithium battery cell are not completely consistent, the terminal voltage of each single lithium battery cell cannot be completely consistent after each charge and discharge, which will cause the If a single battery cell is overcharged or overdischarged in the module, the performance of the single lithium battery cell will deteriorate.

As the number of charging and discharging increases, the degree of deterioration will be further aggravated, and the cycle life will be greatly reduced compared to unmatched single cells. Therefore, in-depth research on the self-discharge rate of lithium-ion batteries is an urgent need for battery production.

Part Ⅰ Factors affecting self-discharge of lithium batteries

The self-discharge phenomenon of the battery refers to the phenomenon that its capacity is spontaneously lost when the battery is left in an open circuit. Lithium battery self-discharge can generally be divided into two types: reversible self-discharge and irreversible self-discharge.

The loss of capacity can be reversibly compensated for reversible self-discharge, the principle is similar to the normal discharge reaction of the battery.

The self-discharge whose loss of capacity cannot be compensated is irreversible self-discharge. The main reason is the irreversible reaction inside the battery, including the reaction between the positive electrode and the electrolyte, the reaction between the negative electrode and the electrolyte, the reaction caused by the impurity in the electrolyte, and the Irreversible reactions caused by micro-short circuits caused by carried impurities, etc.

The factors affecting the self-discharge of lithium batteries are as follows.

1. Cathode material

The influence of the positive electrode material is mainly that the transition metal and impurities of the positive electrode material precipitate in the negative electrode and cause an internal short circuit, thereby increasing the self-discharge of the lithium battery. Yah-Mei Teng et al. studied the physical and electrochemical properties of two LiFePO4 cathode materials. The study found that batteries with high iron impurities in the raw materials and during the charging and discharging process have high self-discharge rate and poor stability. The reason is that iron is gradually reduced and precipitated in the negative electrode, piercing the diaphragm, resulting in a short circuit in the battery, resulting in high self-discharge.

2. Anode material

The influence of the negative electrode material on self-discharge is mainly due to the irreversible reaction between the negative electrode material and the electrolyte. As early as 2003, Aurbach et al. proposed that the electrolyte is reduced to release gas, exposing part of the graphite surface to the electrolyte. During the charging and discharging process, when lithium ions are inserted and extracted, the graphite layered structure is easily destroyed, resulting in a higher self-discharge rate.

3. Electrolyte

The influence of the electrolyte is mainly manifested as: the corrosion of the electrolyte or impurities on the surface of the negative electrode; the dissolution of the electrode material in the electrolyte; the electrode is covered by the insoluble solid or gas decomposed by the electrolyte to form a passivation layer. At present, a large number of scientific researchers are committed to developing new additives to suppress the influence of electrolyte on self-discharge. Jun Liu et al. added VEC and other additives to the MCN111 battery electrolyte and found that the battery's high temperature cycle performance improved, and the self-discharge rate generally decreased. The reason is that these additives can improve the SEI film, thereby protecting the negative electrode of the battery.

4. Storage state

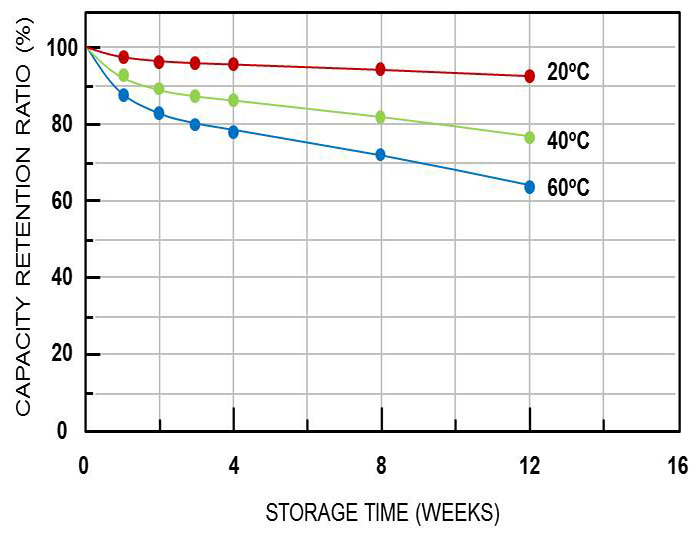
The general influencing factors of storage status are storage temperature and battery SOC. Generally speaking, the higher the temperature, the higher the SOC and the greater the self-discharge of the battery. Takashi et al. conducted capacity decay experiments on lithium iron phosphate batteries under static conditions. The results show that as the temperature increases, the capacity retention rate gradually decreases with the shelf time, and the battery self-discharge rate increases.

Liu Yunjian and others used commercial lithium manganese oxide power batteries and found that as the state of charge of the battery increases, the relative potential of the positive electrode becomes higher and higher, and its oxidizing property becomes stronger; the relative potential of the negative electrode becomes lower and lower. Its reducibility is getting stronger and stronger, and both can accelerate the precipitation of Mn, leading to an increase in the self-discharge rate.

 

5. Other factors

There are many factors that affect the self-discharge rate of the battery. In addition to the ones introduced above, there are mainly the following aspects: during the production process, the burrs generated when the pole pieces are cut, and the impurities introduced into the battery due to production environmental problems, such as Dust, metal powder on the pole piece, etc., all of which may cause the internal micro-short circuit of the battery; the external environment is humid, the external circuit is not completely insulated, and the battery casing is poorly insulated. The battery has an external electronic circuit during storage, which leads to self-discharge; During long-term storage, the bonding between the active material of the electrode material and the current collector fails, causing the active material to fall off and peel off, resulting in a decrease in capacity and an increase in self-discharge. Each of the above factors or a combination of multiple factors can cause the self-discharge behavior of lithium batteries, which makes it difficult to find the cause of self-discharge and estimate the storage performance of the battery.

Part Ⅱ Measurement method of self-discharge rate of lithium battery

Through the above analysis, it can be seen that the self-discharge rate of lithium batteries is generally low. The self-discharge rate itself is affected by factors such as temperature, cycle times, and SOC. Therefore, it is very difficult and time-consuming to accurately measure the self-discharge of the battery.

1. Traditional measurement method of lithium battery self-discharge rate

Currently, there are three traditional methods for detecting self-discharge of lithium batteries:

1.1 Direct measurement

First charge the tested battery to a certain state of charge, and maintain it for a period of time, and then discharge the cell to determine the capacity loss of the battery. Self-discharge rate:

η=(C-C₁)/C*100%

In the formula: C is the rated capacity of the battery; C₁ is the discharge capacity. After the open circuit is left, the remaining capacity of the battery can be obtained by discharging the battery. At this time, perform multiple charge and discharge cycles on the battery again to determine the full capacity of the electric garlic at this time. This method can determine the irreversible capacity loss and reversible capacity loss of the battery.

1.2 Open circuit voltage attenuation rate measurement method

The open circuit voltage is directly related to the SOC of the battery state of charge. It is only necessary to measure the rate of change of the battery's OCV over a period of time, namely:

K= ∆OCV/∆t

The method is simple to operate, and only needs to record the voltage of the battery in any period of time, and then according to the corresponding relationship between the voltage and the battery SOC, the state of charge of the battery at that time can be obtained. Through the calculation of the attenuation slope of the voltage and the corresponding attenuation capacity per unit time, the self-discharge rate of the battery can be finally obtained.

1.3 Capacity retention method

Measure the battery's expected open circuit voltage or the amount of power required by the SOC to obtain the battery's self-discharge rate. That is to measure the charging current while maintaining the open circuit voltage of the battery, and the battery self-discharge rate can be considered as the measured charging current.

2. Quick measurement method of lithium battery self-discharge rate

Because the traditional measurement method requires a long time and the measurement accuracy is insufficient, the self-discharge rate is only used as a method to screen whether the battery is qualified in most cases in the battery testing process. The emergence of a large number of novel and convenient measurement methods has saved a lot of time and energy for the measurement of battery self-discharge.

2.1 Digital control technology

Digital control technology is a new type of self-discharge measurement method derived from the traditional self-discharge measurement method using single-chip microcomputers. This method has the advantages of short measurement time, high accuracy, and simple equipment.

2.2 Equivalent circuit method

The equivalent circuit method is a brand-new self-discharge measurement method, which simulates the battery as an equivalent circuit, which can quickly and effectively measure the self-discharge rate of lithium-ion batteries.

PartⅢ The significance of measuring the self-discharge rate of lithium batteries

As an important performance index of lithium-ion batteries, self-discharge rate has an important influence on battery sorting and matching assembly. Therefore, measuring the self-discharge rate of lithium batteries has far-reaching significance.

1.Test and sort out the problematic battery cells

In the same batch of batteries, the materials and manufacturing controls are basically the same. When the white discharge of individual batteries is obviously too large, the cause is likely to be a serious micro-short circuit caused by impurities and burrs piercing the diaphragm. Because the impact of micro short circuit on the battery is slow and irreversible.

Therefore, the performance of this type of battery in the short term will not differ too much from the normal battery, but after long-term storage, as the internal irreversible reaction gradually deepens, the performance of the battery will be far lower than its factory performance and other normal battery performance. Therefore, in order to ensure the quality of the factory battery, the battery with large self-discharge must be eliminated.

2.Sort the battery cells into groups and then assemble the battery packs

When assembling battery cells into battery packs, the lithium battery cells need better consistency, including capacity, voltage, internal resistance, and self-discharge rate. Therefore, before the battery pack is assembled, a battery cycler system is usually used for battery capacity testing and battery self-discharge rate testing, and then a battery sorting machine is used for cell voltage and internal resistance testing and sorting.

 

The self-discharge rate of the battery affects the battery pack mainly as follows: once assembled into a module, because the self-discharge rate of each single lithium battery is different, the voltage will drop to different degrees during the shelving or cycling process, and in series charging The current will be equal again, so after each charge, there may be overcharged or undercharged single cells in the lithium battery module. As the number of charge and discharge increases, the battery performance will gradually deteriorate, and the cycle life will be similar. Compared with unmatched single cells, it is significantly lower. Therefore, the battery pack requires accurate measurement and screening of the self-discharge rate of lithium-ion battery cells.

3. Lithium battery SOC estimation correction

The state of charge is also called the remaining power, which represents the ratio of the remaining capacity of the battery after a period of use or long-term storage and its fully charged state. It is often expressed as a percentage. The self-discharge rate has important reference value for the SOC estimation of lithium-ion batteries. The correction of the initial SOC value by the self-discharge current can improve the accuracy of SOC estimation. On the one hand, customers can estimate the usable time or driving distance of the product based on the remaining power; on the other hand, improving the SOC prediction accuracy of BMS can effectively prevent battery overcharge. Overdischarge, thereby extending battery life.